Introduction
I’ve been thinking about representational complexity for a long time, and in fact one of the first papers I wrote was on the intersection number of an infinite graph. Despite literally 20 years of thinking on the subject, for some reason, I wasn’t until today able to accurately think about the Kolmogorov Complexity of a graph. Sure, it’s a complex topic, but the answer is pretty trivial. Specifically, every graph can be represented as an 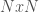 matrix, where
matrix, where  is the number of vertices. However, this is obviously too big of a structure to be the K-complexity, since it contains duplicate entries (I’m assuming it’s an undirected graph with no loops). That is, entry
is the number of vertices. However, this is obviously too big of a structure to be the K-complexity, since it contains duplicate entries (I’m assuming it’s an undirected graph with no loops). That is, entry 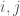 in the matrix is the same as entry
in the matrix is the same as entry 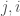 , and as such contributes no new information about the graph. Therefore, the K-complexity of a graph must be less than
, and as such contributes no new information about the graph. Therefore, the K-complexity of a graph must be less than 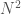 .
.
We can improve our measure of K-complexity by noting that any graph can be described by simply listing its edges. For example, a complete graph on three vertices can be represented by the set of vectors 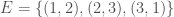 . That is, each vector represents an edge, and the digits in the vector tell you the labels of the vertices connected by the edge in question. In this case
. That is, each vector represents an edge, and the digits in the vector tell you the labels of the vertices connected by the edge in question. In this case 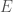 connects vertex
connects vertex 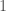 to
to 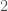 ,
, 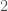 to
to 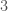 , and
, and 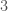 to
to 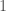 , producing a circuit on three vertices, i.e., a complete graph on three vertices. As a consequence, the K-complexity of a graph cannot exceed the complexity of its edge set. Each label in a graph will be less than the order of the graph (i.e., the number of vertices
, producing a circuit on three vertices, i.e., a complete graph on three vertices. As a consequence, the K-complexity of a graph cannot exceed the complexity of its edge set. Each label in a graph will be less than the order of the graph (i.e., the number of vertices  ), and as a result, we can encode each label in the edge set with at most
), and as a result, we can encode each label in the edge set with at most  bits. Each edge consists of two labels, and so the K-complexity of a graph must be less than or equal to
bits. Each edge consists of two labels, and so the K-complexity of a graph must be less than or equal to 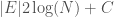 .
.
Structural Complexity
Note that  is again an upper bound on the K-complexity of a graph, it’s just much better than
is again an upper bound on the K-complexity of a graph, it’s just much better than 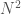 , since it at least takes into account the number of edges, and uses a more efficient representation of the graph. However, particular graphs can definitely be expressed in fewer bits. Specifically, the empty graph, the complete graph, and a Hamiltonian circuit, each of a given order
, since it at least takes into account the number of edges, and uses a more efficient representation of the graph. However, particular graphs can definitely be expressed in fewer bits. Specifically, the empty graph, the complete graph, and a Hamiltonian circuit, each of a given order  , can be expressed in
, can be expressed in 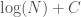 bits, where
bits, where 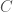 is a constant that is the length of the program that constructs the graph, which we can think of as simply generating the list of edges that defines the graph. For example, the following Octave Code will generate a Hamiltonian circuit of any order
is a constant that is the length of the program that constructs the graph, which we can think of as simply generating the list of edges that defines the graph. For example, the following Octave Code will generate a Hamiltonian circuit of any order  :
:
E{1} = (1,N);
for i = 2 : N – 1
E{i} = (i, i+1);
endfor
As a result, we can produce a Hamiltonian circuit of any order, using at most 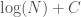 bits, where
bits, where 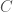 is the length of the program above in bits. Analogous code will produce a complete graph, whereas an empty graph can be produced by simply specifying
is the length of the program above in bits. Analogous code will produce a complete graph, whereas an empty graph can be produced by simply specifying  (i.e., there are no edges), which again requires exactly
(i.e., there are no edges), which again requires exactly 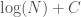 bits, but using different code. Note that even in these cases, it’s still possible that an even shorter, presumably not universal program produces a given graph as its output when fed as the input to a UTM. That is, e.g.,
bits, but using different code. Note that even in these cases, it’s still possible that an even shorter, presumably not universal program produces a given graph as its output when fed as the input to a UTM. That is, e.g.,  , where
, where  is a binary string,
is a binary string, 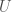 is some UTM, and
is some UTM, and 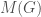 is the matrix that defines the graph
is the matrix that defines the graph  . As a theoretical matter, the length of
. As a theoretical matter, the length of  could be even smaller than
could be even smaller than  , where again
, where again  is the order of
is the order of  . This would be true for empty graphs, complete graphs, and Hamiltonian circuits of order
. This would be true for empty graphs, complete graphs, and Hamiltonian circuits of order  , where the number
, where the number  itself is highly compressible.
itself is highly compressible.
Kolmogorov-Random Graphs
It turns out it’s pretty easy to prove that Kolmogorov-Random Graphs exist, in the sense that we can produce graphs using Kolmogorov-Random strings. There’s obviously scholarship on point, but I think the ideas I’ve set out in this note are a lot easier to think about, and unify perfectly with the complexity of strings. Specifically, recall that we can represent any graph using its edge set. If we modify the method used to do so above, we can show that Kolmogorov-Random strings will produce graphs when fed as inputs to a UTM, which implies that those graphs are literally Kolmogorov-Random, in the same sense as a binary string.
Returning to the example of a complete graph on three vertices above, let’s represent that graph using three sets: the set of vertices adjacent to 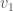 , the set of vertices adjacent to
, the set of vertices adjacent to  , and the set of vertices adjacent to
, and the set of vertices adjacent to 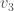 . Because it’s a complete graph on three vertices, we would have the following:
. Because it’s a complete graph on three vertices, we would have the following: 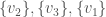 . Note that as we move forward in the labels, e.g., from vertex
. Note that as we move forward in the labels, e.g., from vertex 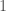 to vertex
to vertex 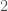 , we gain information about the graph. Specifically, there’s no reason to include
, we gain information about the graph. Specifically, there’s no reason to include 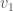 in the set of vertices adjacent to
in the set of vertices adjacent to  , since that information is contained in the set of vertices adjacent to
, since that information is contained in the set of vertices adjacent to 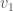 . As a result, the maximum number of elements in the set for
. As a result, the maximum number of elements in the set for 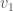 is
is 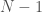 , and for
, and for  it’s
it’s  , and so on. As a result, we can represent the graph as a “matrix” where the number of columns begins at
, and so on. As a result, we can represent the graph as a “matrix” where the number of columns begins at 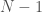 for
for 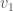 , and decreases by
, and decreases by 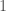 for each row. Note that as a result, the
for each row. Note that as a result, the  -th row has no columns, implying that the “matrix” has
-th row has no columns, implying that the “matrix” has 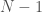 rows. We can treat every entry in this “matrix” as a binary number indicating the presence or absence of a given edge. For example, if entry
rows. We can treat every entry in this “matrix” as a binary number indicating the presence or absence of a given edge. For example, if entry 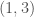 is
is 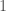 , then edge
, then edge 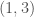 is included in the graph. This is just like a regular graph matrix, except it contains no duplicate entries, and therefore the number of columns is not constant. Note that therefore, it corresponds to a binary string of length
is included in the graph. This is just like a regular graph matrix, except it contains no duplicate entries, and therefore the number of columns is not constant. Note that therefore, it corresponds to a binary string of length 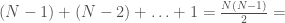
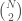 , which is also the maximum number of edges.
, which is also the maximum number of edges.
Let  be a Kolmogorov-Random string of length
be a Kolmogorov-Random string of length 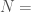
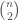 . All we have to do is restructure
. All we have to do is restructure  into the shape of a “matrix” described above, which will produce a graph
into the shape of a “matrix” described above, which will produce a graph  . Because
. Because  is Kolmogorov-Random, there cannot be another binary string shorter than
is Kolmogorov-Random, there cannot be another binary string shorter than  that will generate
that will generate  on a UTM, by which we mean generating the edges of
on a UTM, by which we mean generating the edges of  . Assume such a string
. Assume such a string 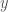 exists. It follows that
exists. It follows that 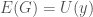 , which in turn will allow us to construct a “matrix” of the type above, which will in turn produce
, which in turn will allow us to construct a “matrix” of the type above, which will in turn produce  . Because
. Because  is Kolmogorov-Random, there cannot be a string shorter than
is Kolmogorov-Random, there cannot be a string shorter than  that generates
that generates  , yet
, yet 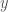 is exactly such a string, which produces a contradiction, completing the proof.
is exactly such a string, which produces a contradiction, completing the proof.
Note that such a graph  cannot be a complete graph, since a complete graph has a trivial complexity, as we’ve seen above. It is therefore interesting that a Kolmogorov-Random Graph has a Kolmogorov Complexity of exactly the number of edges in a complete graph of the same order. Because not all numbers are of the form
cannot be a complete graph, since a complete graph has a trivial complexity, as we’ve seen above. It is therefore interesting that a Kolmogorov-Random Graph has a Kolmogorov Complexity of exactly the number of edges in a complete graph of the same order. Because not all numbers are of the form 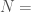
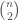 , we cannot say that the Kolmogorov Complexity of a Kolmogorov Random graph is always the number of edges in a complete graph of the same order, though it might nonetheless be true.
, we cannot say that the Kolmogorov Complexity of a Kolmogorov Random graph is always the number of edges in a complete graph of the same order, though it might nonetheless be true.
Computability and Infinite Sets of Graphs
Let 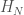 denote the Hamiltonian circuit of order
denote the Hamiltonian circuit of order  , and let
, and let 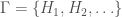 . Despite the fact the set is infinite, because each such graph has a simple structure, we can define a computable test that will allow us to determine whether a graph
. Despite the fact the set is infinite, because each such graph has a simple structure, we can define a computable test that will allow us to determine whether a graph  is in that set, or not. Just to sketch the algorithmic test, we would begin by testing the degree of each vertex in
is in that set, or not. Just to sketch the algorithmic test, we would begin by testing the degree of each vertex in  , and if it’s not
, and if it’s not 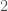 , the algorithm terminates and returns “false”. If the degree of each vertex is in fact
, the algorithm terminates and returns “false”. If the degree of each vertex is in fact 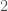 , then we traverse the edges of the graph, and if we don’t return to the original vertex, we again return “false”, otherwise we return “true”. As a result, there is a computable test that allows us to state whether or not a given graph
, then we traverse the edges of the graph, and if we don’t return to the original vertex, we again return “false”, otherwise we return “true”. As a result, there is a computable test that allows us to state whether or not a given graph  is in
is in 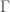 . Note that as a consequence, we can also generate
. Note that as a consequence, we can also generate 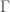 , using brute force, producing all graphs of orders
, using brute force, producing all graphs of orders 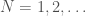 and testing which of those belong in
and testing which of those belong in 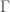 . Similarly, as noted above, we can algorithmically construct a Hamiltonian circuit of all orders, and can therefore, test whether or not a given graph is in the set of graphs generated by that process. Note that the constructive algorithm above, is very different from the algorithmic test we just articulated in this section. Therefore, we have an interesting equivalence, in that the existence of an algorithmic test implies a constructive algorithm (via brute force), and a constructive algorithm implies an algorithmic test (again via brute force, e.g., in the case where there are multiple graphs of a given order).
. Similarly, as noted above, we can algorithmically construct a Hamiltonian circuit of all orders, and can therefore, test whether or not a given graph is in the set of graphs generated by that process. Note that the constructive algorithm above, is very different from the algorithmic test we just articulated in this section. Therefore, we have an interesting equivalence, in that the existence of an algorithmic test implies a constructive algorithm (via brute force), and a constructive algorithm implies an algorithmic test (again via brute force, e.g., in the case where there are multiple graphs of a given order).
At the same time, because the set of graphs is countably infinite, and the set of algorithms is countably infinite, the number of infinite subsets of the set of all graphs is uncountable and therefore larger than the set of all algorithms. Therefore, it must be the case that there are infinite sets of graphs that do not have an algorithmic test, and therefore do not have a constructive algorithm. One simple example follows from the existence of non-computable infinite strings. Again, the set of all infinite binary strings is uncountable, whereas the set of all algorithms is countable. As a consequence, there must be infinite strings that cannot be generated by a finite program running on a UTM.
Let  be such a non-computable infinite string. Define
be such a non-computable infinite string. Define 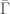 as the subset of
as the subset of 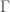 such that
such that  is included in
is included in 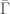 if
if  . That is, where
. That is, where  , we include the corresponding element of
, we include the corresponding element of 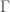 . As noted above, there is a simple algorithmic test to determine whether or not each element of
. As noted above, there is a simple algorithmic test to determine whether or not each element of 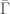 is Hamiltonian, but this is distinct from an algorithmic test that determines whether or not a given graph
is Hamiltonian, but this is distinct from an algorithmic test that determines whether or not a given graph  , is in
, is in 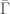 . That is, not all Hamiltonian circuits are in
. That is, not all Hamiltonian circuits are in 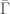 . Now assume that such an algorithmic test
. Now assume that such an algorithmic test  exists. It follows that we can then generate every Hamiltonian circuit starting with
exists. It follows that we can then generate every Hamiltonian circuit starting with  , and
, and  will tell us whether or not that particular order is included in
will tell us whether or not that particular order is included in 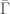 . If
. If  is included, set binary string entry
is included, set binary string entry 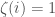 and otherwise set
and otherwise set 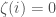 . It follows that
. It follows that  . However, we generated
. However, we generated 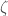 on a UTM, which is not possible, since
on a UTM, which is not possible, since  is by definition non-computable, which leads to a contradiction. This implies
is by definition non-computable, which leads to a contradiction. This implies  does not exist. This demonstrates that even if a set is computable, it will have non-computable subsets, just like the natural numbers, and all countable sets generally.
does not exist. This demonstrates that even if a set is computable, it will have non-computable subsets, just like the natural numbers, and all countable sets generally.
Properties without Computable Tests
In the previous section I noted that Hamiltonian circuits are simple structures, and therefore, we can come up with simple algorithms that test for whether or not a graph is a Hamiltonian circuit. Testing whether or not a given graph contains a Hamiltonian circuit as a subgraph is believed to be intractable. As such, there are simple structures that correspond to simple algorithms, though finding simple structures in more complex graphs is suddenly intractable. This raises the question of whether or not there are properties that cannot be tested for algorithmically at all. The answer is yes.
Order the set of all finite graphs  , and let
, and let  be an infinite binary string. If
be an infinite binary string. If 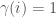 , then we can interpret this as
, then we can interpret this as 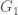 having property
having property  given the ordering, or equivalently, view
given the ordering, or equivalently, view  as defining a set of graphs. There are again more binary strings than there are algorithms, and therefore, in this view, more properties than there are algorithms. The question is whether there are more interesting and / or useful properties than there are algorithms, but the bottom line is, the number of properties is uncountable, and therefore the density of testable properties is zero. You might be tempted to say that all such properties are uninteresting, or not useful, but unfortunately, whether or not a program will halt is precisely one of these properties, which is both useful and interesting, suggesting at least the possibility of other such useful and interesting properties.
as defining a set of graphs. There are again more binary strings than there are algorithms, and therefore, in this view, more properties than there are algorithms. The question is whether there are more interesting and / or useful properties than there are algorithms, but the bottom line is, the number of properties is uncountable, and therefore the density of testable properties is zero. You might be tempted to say that all such properties are uninteresting, or not useful, but unfortunately, whether or not a program will halt is precisely one of these properties, which is both useful and interesting, suggesting at least the possibility of other such useful and interesting properties.
The Distribution of Graph Properties
Ramsey Theory is one of the most astonishing fields of mathematics, in particular, because like all combinatorics, it has intrinsic physical meaning, in that combinatorics provides information about the behavior of reality itself. What’s astonishing about Ramsey Theory in particular, is that it’s fair to say that it shows that structure increases as a function of scale, in that as objects get larger, they must have certain properties. What I realized today, is that the number of properties that they can have also grows as a function of scale. For intuition, consider all graphs on 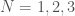 vertices. You can see right away that the complete graph on
vertices. You can see right away that the complete graph on 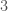 vertices is the smallest possible Hamiltonian circuit, and therefore, the smallest Hamiltonian graph. It is simply not possible to have a Hamiltonian graph with fewer vertices. This suggests the possibility that the number of properties that a graph can have grows as a function of its order, and we show using some not terribly impressive examples, that this in fact must be true, suggesting the possibility, that useful and interesting properties of objects continue to arise as a function of their scale.
vertices is the smallest possible Hamiltonian circuit, and therefore, the smallest Hamiltonian graph. It is simply not possible to have a Hamiltonian graph with fewer vertices. This suggests the possibility that the number of properties that a graph can have grows as a function of its order, and we show using some not terribly impressive examples, that this in fact must be true, suggesting the possibility, that useful and interesting properties of objects continue to arise as a function of their scale.
Let  be an infinite binary string, and define an infinite subset of the natural numbers
be an infinite binary string, and define an infinite subset of the natural numbers  such that
such that 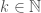 is included in
is included in  if
if 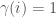 . Now define an infinite set of graphs
. Now define an infinite set of graphs 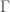 such that
such that  is in
is in 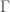 if the number of edges of
if the number of edges of  is divisible by
is divisible by  . Because each
. Because each  is a Hamiltonian circuit, the number of edges in
is a Hamiltonian circuit, the number of edges in  is simply
is simply  . Putting it all together, we have an infinite set of graphs, each of which are Hamiltonian circuits of different orders, and whether or not a given order is included in the set, is determined by whether or not that order is divisible by the corresponding integer value in
. Putting it all together, we have an infinite set of graphs, each of which are Hamiltonian circuits of different orders, and whether or not a given order is included in the set, is determined by whether or not that order is divisible by the corresponding integer value in  . Note that larger graphs will have orders that are divisible by more numbers, though the number of divisors does not increase monotonically as a function of
. Note that larger graphs will have orders that are divisible by more numbers, though the number of divisors does not increase monotonically as a function of 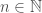 . Therefore, in this view, larger graphs have more properties in the sense of being included in more sets of this type.
. Therefore, in this view, larger graphs have more properties in the sense of being included in more sets of this type.
Complexity Versus Computability
Intuitively, there is a connection between complexity and computability. In at least one case, this is true, in that the Kolmogorov Complexity of a non-computable infinite string is countable. That is, if a string is non-computable, then there is no finite input to a UTM that will generate that string. As a result, its complexity cannot be finite. At the same time, we can simply copy the string from the input tape, to the output tape, assuming both are infinite tapes. Therefore, the Kolmogorov Complexity of a non-computable infinite string is countable. However, this intuition is subject to more careful examination in the case of infinite sets, in that you can construct non-computable sets of low-complexity objects.
Now assume that  from the example in the previous section is non-computable, which implies that both
from the example in the previous section is non-computable, which implies that both  and
and 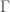 are non-computable. As discussed above, it follows that there is no computable test for inclusion in
are non-computable. As discussed above, it follows that there is no computable test for inclusion in 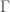 . At the same time, each of the graphs in
. At the same time, each of the graphs in 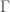 is a Hamiltonian circuit, with a Kolmogorov Complexity of
is a Hamiltonian circuit, with a Kolmogorov Complexity of 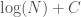 . Note that the ratio
. Note that the ratio 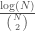 approaches zero as
approaches zero as  approaches infinity. As such, we have an infinite set of graphs that is non-computable, but each of the individual graphs are low-complexity objects, though note that the set was generated using a non-computable string.
approaches infinity. As such, we have an infinite set of graphs that is non-computable, but each of the individual graphs are low-complexity objects, though note that the set was generated using a non-computable string.
