June | 2019 | Information Overload

In a previous note, I introduced an algorithm that can, without any dataset or other prior information, reassemble a scrambled image to its original state. In this note, I’m going to introduce a related algorithm that can quickly find boundaries in an image without any dataset.

Though I’ve yet to formally analyze the run time of the boundary detection algorithm, it is remarkably fast, and certainly a low-degree polynomial. I suspect this algorithm will have applications in real-time object tracking, lane detection, and probably machine generated art.

The core insight of both algorithms is that real life objects are generally structured in a manner that causes colors to be locally consistent. That is, if we look closely at an object, we’ll find that color palettes that are proximate in space are generally similar. Therefore, as we traverse an image in a given direction, if we find that the color palette changes sharply, then we’ve probably transitioned to a new region of the image.

Both algorithms measure local color consistency using a vectorized implementation of set intersection that I’ve developed. Specifically, both test how many colors two regions have in common by taking the intersection of the color sets in the two regions. However, unlike ordinary intersection, these algorithms measure what I call the “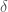 $\delta$ -intersection” of two sets, which, rather than test for equality, tests whether the norm of the difference between two color vectors is less than some value 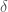$\delta$ . If the norm of the difference is less than 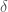$\delta$ , then the two colors are treated as “the same” for purposes of calculating the intersection between the two sets that contain the colors in question.

This value of 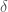$\delta$ is optimized using the same methods that I introduced previously, which make use of information theory, producing a context-dependent level of distinction that allows us to say whether any two given colors are close enough to be considered the same. You can find an overview of my work in artificial intelligence in my research paper, A New Model of Artificial Intelligence.

How it works

This is just a high level summary, as I’m leaving Sweden tomorrow for New York City, and plan to write a comprehensive, formal research paper on all of my work on color processing and color perception, which is at this point, extensive.

The first step is to break up the image into rectangular regions using my core image partition algorithm. This will impose a grid upon the image that already contains the macroscopic boundaries of the objects within the image, but because it’s structured as a grid, it also contains edges that don’t correspond to actual boundaries. The example below shows a photograph I took in Williamsburg, Brooklyn, of a small brick wall, together with the image as broken into regions by the partition algorithm. The image on the right shows the average color of each region generated by the partition algorithm, as a visual aid.

The original image.

The average color of each region in the original image.

The next step is to go through each of these regions, first by “reading” each row of the partition from left to right, and calculating the 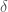$\delta$ -intersection of the colors contained in neighboring regions. So beginning with the top left region of the image, which is mostly white, we calculate the 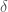$\delta$ -intersection between that region and the region to its immediate right, which is also mostly white. As we transition from left to right, we’re going to eventually reach regions that have a darker tone, causing the intersection count to start to drop off. As you can see, regions (1,3) and (1,4) have significantly different coloring, which is going to cause the 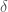$\delta$ -intersection count to suddenly drop off, suggesting that there’s a boundary, which is actually the case.

All of my work so far in artificial intelligence has made use of finite differences to construct categories, and more generally, distinguish between objects. For example, the value of 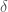$\delta$ above that we use to distinguish between colors is a fixed value that is intended to be used as a limit on the difference between two vectors, above which, we distinguish. I’ve coined the term minimum sufficient difference to describe this concept of 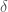$\delta$ generally. That is, in this case, 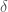$\delta$ is the minimum sufficient difference between two color vectors necessary to distinguish between the colors. In simple terms, if the difference between two colors is more than 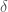$\delta$ , then they’re not the same in the context of the image, and their difference exceeds the minimum sufficient difference for distinction in that context.

However, when “reading” an image from left to right, there might not be a single minimum sufficient difference between intersection counts capable of identifying all of the boundaries in an image. As a simple example, consider the following sequence of integers:

1, 2, 5, 107, 210, 250.

Let’s pick a fixed value of $\delta = 6$ . Reading this sequence from left to right, and calculating the difference between adjacent entries, we would place delimiters as follows:

1, 2, 5 || 107 || 210 || 250.

If these numbers represent the intersection counts between neighboring regions in an image, then this partition is probably wrong, since the numbers 107, 210, and 250, probably all correspond to a single, new region that begins at 107. That is, the correct partition is probably the following:

1, 2, 5 || 107, 210, 250.

This partition cannot be produced using a fixed finite difference. Specifically, since 5 and 107 are categorized separately, it must be the case that 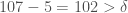$107 - 5 = 102 > \delta$ . Because 107 and 210 are categorized together, it must be the case that 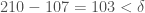$210 - 107 = 103 < \delta$ . But obviously, it cannot be the case that 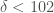$\delta < 102$ and $\delta > 103$ . Nonetheless, we might need to produce this partition, so as a result, the boundary algorithm makes use of a ratio test, rather than a finite difference test. Specifically, it tests the ratio between the intersection counts of neighboring regions.

Continuing with the sequence of integers above, we would calculate the ratio between 1 and 2 (.5), 2 and 5 (.4), 5 and 107 (.0467), 107 and 210 (.5095), and 210 and 250 (.84). Using this approach, we can fix a minimum ratio of $\Delta = .4$ , which will cause us to draw a boundary at the right place, between 5 and 107.

Applying this approach to the original image of the wall generates the following partition:

The original image.

I’ve come up with a method of optimizing 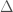$\Delta$ that you can see in the code, which is available in my code bin (see, “delimit_image”). I’ll follow up with a feature extraction algorithm based upon this technique, that will identify contiguous regions in an image.

I’ll explain all of this in greater detail from the other side of the Atlantic, in New York City. In the interim, here are three more examples of boundaries generated by the algorithm: