CORRECTION: A Note on Testing Vectorization

In addition to vectorizing my algorithms, I’ve been trying to understand why vectorization matters on a consumer device, and the obvious answer is vectorization makes use of the capacity of a machine to compute in parallel, rather than serial.

However, I realized that I screwed up the code in my first note on the subject, producing what looks like a constant run time –

This is simply wrong, so I took the article down.

What I now believe is that there is parallel capacity, even in consumer devices, but that it’s so small, you end up with a linear run time, not a constant run time, for vectorized operators. Specifically, it seems that vectorized operators can’t process an entire pair of vectors at the same time, but many of the operations are processed simultaneously, possibly implemented as a loop with a drastically smaller number of iterations at a lower level in the language.

I’m now conducting a more careful analysis of the runtimes of basic operations in Octave / Matlab, and I’m also going to have a look at the documentation. The bottom line is, vectorized operators are expressed as array operators, and are plainly more efficiently implemented than iteratively applying operators.

Fully Vectorized Delta-Clustering

I’ve been on a Zen-Mission of sorts, fully vectorizing my algorithms, and I’ve just implemented code for vectorizing my within-delta clustering technique, and the results so far are quite good, and the code is just 28 lines long in Octave.

Testing it on the UCI Iris Dataset (150 rows), the runtime is 0.00972605 seconds, and the accuracy is 0.99529.

Testing it on the UCI Ionosphere Dataset (351 rows), the runtime is 0.180258 seconds, and the accuracy is 0.99972.

Testing it on the MNIST Numerical Dataset (1000 rows), the runtime is 7.04497 seconds, and the accuracy is 1.

function [cluster_matrix final_delta] = fully_vectorized_delta_clustering(dataset, N)
dataset = dataset(:,1:N);
num_rows = size(dataset,1);
num_cols = size(dataset,2);
s = std(dataset(:,1:N)); %calculates the standard deviation of the dataset in each dimension
s = mean(s); %takes the average standard deviation
alpha = 1.5; %this is a constant used to adjust the standard deviation
s = s*alpha;
num_iterations = 25; %this is a hypothetical that is vectorized
temp_matrix = repmat(dataset’, [1 1 num_rows]);
ref_dataset = shiftdim(temp_matrix,2);
diff_matrix = (dataset(:,1:N) .- ref_dataset).^2;
diff_vector = sum(diff_matrix,2);
delta_vector = [1/num_iterations : s/num_iterations : s];
delta_vector = delta_vector.^2;
num_delta_tests = size(delta_vector,2);
delta_matrix = repmat(delta_vector, [num_rows 1]); %housekeeping repitition of the entries in delta_vector
final_matrix = diff_vector < delta_matrix;
LH = final_matrix(:,1:num_delta_tests – 1, :);
RH = final_matrix(:,2:num_delta_tests,:);
change_count_matrix = (LH .- RH).^2; %counts the number of times a test condition changes
change_count_vector = sum(change_count_matrix,1); %takes the sum over the changes by column
change_count_vector = sum(change_count_vector,3); %takes the sum over the changes by page
[a b] = max(change_count_vector);
final_delta = delta_matrix(1,b);
final_delta = final_delta(1,1);
cluster_matrix = diff_vector < final_delta;
endfunction

cmndline_vect_clust-1Download

fully_vectorized_delta_clusteringDownload

New Book: VeGa

I’ve started a third book, VeGa, that again likely won’t be done anytime soon, that I’m chipping away at in my free time.

This text is a mix between heavily autobiographical material, and what I’m hoping will be in essence a science fiction book, that projects my work in A.I. and physics well into the future.

Enjoy!

VeGaDownload

Vectorized Prime Number Testing

So I realized last night, that you can probably find Hamiltonian circuits quickly, using vectorization / parallel computing, and tonight, I realized you can also test for whether a number is prime using vectorization, and the results are pretty impressive, and below is some command line code, together with the runtimes, which are in the fractions of a second until you hit the double digit millions, which took just over one second:

ostensible_prime = 7;

tic; [is_prime divisor_vector] = prime_test(ostensible_prime); toc

0.000156164 seconds.

ostensible_prime = 16127;

tic; [is_prime divisor_vector] = prime_test(ostensible_prime); toc

0.000491858 seconds.

ostensible_prime = 27644437;

tic; [is_prime divisor_vector] = prime_test(ostensible_prime); toc

1.00698 seconds.

The code is attached below.

prime_testDownload

Nearest Neighbor Clustering

Following up on my previous post, below is code that generates clusters given the nearest neighbors of a dataset. This ends up generating clusters for each vector, and also, a graph for the entire dataset, that represents how vectors are connected to one another through being the nearest neighbors of one another.

To generate a cluster, simply take the i-th row of the graph matrix, and that row will tell you which vectors generated row i as their nearest neighbor.

I just posted something related on Twitter, regarding graph entropy, and it dawned on me, that it’s impossible for the resultant graph to be complete –

Every vector will have a nearest neighbor, and therefore, the out-degree of every vertex in the resultant graph (this is a directed graph) is greater than zero, and exactly one. However, if any vector is the nearest neighbor of every other vector, then all vectors point to that single vector (the “hub vector”), and therefore, no other vector can be the nearest neighbor of any other vector, other than the one vector that is the nearest neighbor of the hub vector.

In fact, if this is the case, then there is necessarily a directed loop in the graph, from the hub vector, to its nearest neighbor, and back.

function graph_matrix = generate_NN_graph(dataset, nearest_neighbors, N)

num_rows = size(dataset,1);
graph_matrix = zeros(num_rows,num_rows);
for i = 1 : num_rows
a = find(nearest_neighbors == i);
graph_matrix(i,a) = 1;
endfor

endfunction

Fully Vectorized Nearest Neighbor

I’ve reduced the nearest neighbor method to 10 lines of code in Octave / Matlab:

function nearest_neighbors = NN_fully_vectorized(dataset, N)

dataset = dataset(:,1:N); %removes the hidden classifier
num_rows = size(dataset,1);
num_cols = size(dataset,2);
temp_matrix = repmat(dataset’, [1 1 num_rows]);
ref_dataset = shiftdim(temp_matrix,2);
diff_matrix = sum((dataset.-ref_dataset).^2,2);
zero_indeces = 1:num_rows+1:num_rows*num_rows;
diff_matrix(zero_indeces) = Inf; %sets the zero entries to infinity
[a b] = min(diff_matrix);
nearest_neighbors = reshape(b,[num_rows 1]);

endfunction

A Thought on Epistemology

Geometry, like combinatorics, is absolute –

The problem is human error.

If you were able to draw a perfect triangle, and measure it perfectly, you would find the Pythagorean theorem holds, perfectly, if you assume the universe is at least countably infinite, which would produce no real number error, if the triangle is drawn with countable precision.

Empiricism suggests the same –

The more precisely we draw, and the more precisely we measure, the more consistent observation is with mathematics. It also suggests the possibility that physics is absolute, and simply unknown to us.

There is combinatorics, which is plainly absolute, with no possible deviations, since it requires only finite discernment, and a finite number of observations –

Simply counting.

In contrast, Geometry requires an infinite number of points, and is therefore not observably absolute, like combinatorics, but because it requires only finite length proofs, it is absolute as an idea, in that you can prove in a finite number of steps, any knowable claim about a geometric object.

Physics requires infinite observation to know with certainty, and therefore, it is not possible to know without infinite time, whether a given model of physics is truly absolute.

This creates a hierarchy of knowledge:

1. Combinatorics, known to be absolute.
2. Geometry, known to be absolute as an idea.
3. Physics, cannot be known as absolute in finite time.

However, if the Universe is for example countably infinite, and if your perspective were infinitesimal, able to make infinitesimal measurements, then you would see the imperfections in what appear to be perfect curves, since you would see the local linearity of a curve that is perfect from our perspective, which is limited to computable measurement.

Information, Knowledge, and Uncertainty

In a previous article, I introduced a rigorous method for thinking about partial information, though for whatever reason, I left out a rather obvious corollary, which is that you can quantify both uncertainty and knowledge in terms of information, though I did go on a rant on Twitter, where I explained the concept in some detail.

Though I’ve done a ton of work on the issue, which I’ll expand upon in other articles, the fundamental equation that follows is,

,

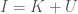Where 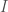is the total information of the system, is the subjective knowledge with respect to the system, held by some observer, and 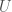is the uncertainty of that same observer with respect to the system, all having units of bits.

To develop an intuition for the equation, consider a set of labeled boxes, one of which contains a pebble. The system of the boxes and single pebble can be in any one of states, since the pebble can be in any one of the boxes, with each such configuration representing a unique state of the system. As a storage device, the system can be in any one of states, and can, therefore, store bits of information.

I am plainly making the assumption that this is the correct measure of the information content of the system as described. What cannot be debated is the fact that the system, as described, can be used to store bits. Moreover, as a general matter, the storage capacity of any system is always given by the logarithm of the number of states of the system, and so, though there could be other useful measures of the information content of a physical system, the log of the number of states of the system is both objectively, and physically meaningful.

Returning to the example of the pebble in one of boxes, imagine you have no information at all about which box contains the pebble, and no knowledge of the probabilities that the pebble is in a given box. In this case, your knowledge is exactly zero, and so your uncertainty is maximized at . If we increase , we increase your uncertainty, which as a practical matter, is exactly what would happen, since you now have more possible outcomes. Stated more formally, the system can be in a greater number of states, which as a mathematical and practical matter, increases your uncertainty with respect to the system.

You can read through the previous article to understand the mathematics of how knowledge changes as a function of observation and receipt of information, but the intuition is straightforward: learning about a system eliminates possible states of the system. For example, if I tell you that the pebble is in the first box, then it isn’t in the rest of them, and your uncertainty drops to zero. If I tell you that the pebble isn’t in the first box, then your uncertainty decreases, but is still greater than zero.

Now imagine there are 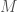pebbles, and boxes, for some . It follows that this system can be in states. Intuitively, your uncertainty should follow the arc of the binomial coefficient, as a function of 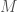, increasing for some time, and then eventually decreasing again past . Again, this causes the measure of uncertainty introduced above to change in a manner that is consistent with intuition, in that the more states a system can be in, the greater your uncertainty is with respect to the system.

In Shannon’s original paper, in addition to introducing entropy as a measure of minimum average encoding length, he also proved that the equation satisfies a sensible definition of uncertainty. If you apply this idea to physical systems, what you end up with is an equivalence between the minimum average code length required to represent the system, and the uncertainty of an observer with respect to the system.

Again, these are assumptions that make use of underlying mathematical theorems, and are not theorems in and of themselves. Said otherwise, you could argue that physical uncertainty is not appropriately measured by the Shannon entropy, or the ideas I’ve introduced above, and in the previous article, which is fine. My goal is to present a practical measure of uncertainty, that moves in the correct direction, as a function of observation, and receipt of information, understanding that it may not even be possible to prove a physical claim of this type in any decisive manner.

It follows that if is the number of states of the system, then simply substituting uncertainty with Shannon’s equation for entropy, we have,

,

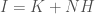where .

So just a matter of simple algebra, we have that,

.

This is consistent with intuition, in that as the entropy of a probability distribution decreases, you have more knowledge about the behavior of the system ex ante. In the extreme case, where the system is almost certain to be in a particular state, you have almost perfect knowledge about its behavior, since you can reliably expect it to be in that particular state.

Returning to the example above, let’s assume that the pebble is almost certain to be in the first box. This implies that the entropy of the probability distribution of the location of the pebble will be approximately zero, which in turn implies almost perfect knowledge about the system. This is consistent with intuition, since you can reasonably expect the pebble to be in the first box, basically all the time.