Imagine we had a line segment with a finite length, and then iteratively extracted the center  ; and then extracted the center
; and then extracted the center  of the two resulting segments, and so on.
of the two resulting segments, and so on.
The set of points that remains after this process is of course the Cantor Set:
https://en.wikipedia.org/wiki/Cantor_set
Note that this set will be bounded by the two end points of the original line segment.
Now imagine that we gave the line segment some velocity, sending the entire Cantor Set in between, in tact, through space. Further, imagine that we had a sensor at a fixed point along the path of the set that lights up every time a point in the set crosses the sensor.
Because there are a countable number of gaps in the line segment, the light will blink on and off with some frequency, an infinite number of times. The signal generated will depend upon both the gaps in the set, and the velocity of the line segment.
Also note that the amount of time it takes for the line segment to cross the sensor is given by 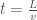 , where
, where 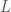 is the length of the segment, and
is the length of the segment, and  is the velocity of the segment. Because
is the velocity of the segment. Because 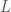 and
and  are both finite,
are both finite,  is finite.
is finite.
Now imagine that we have two such line segments 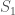 and
and 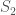 , both of length
, both of length 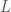 , but that
, but that 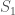 is travelling with a faster velocity of
is travelling with a faster velocity of  . Because
. Because  , it will take less time for
, it will take less time for 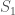 to cross the sensor, causing the sensor to be triggered for a shorter amount of time by
to cross the sensor, causing the sensor to be triggered for a shorter amount of time by 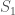 than
than 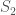 .
.
For example, the length of the gap in the middle (the largest gap initially removed) has a length of  . The amount of time it takes for this gap to cross the sensor is
. The amount of time it takes for this gap to cross the sensor is  , which will obviously depend upon the velocity of the segment. If we assume that the light turns off once the sensor hits this gap, then the amount of time the light is off during this gap will vary with the velocity of the segment.
, which will obviously depend upon the velocity of the segment. If we assume that the light turns off once the sensor hits this gap, then the amount of time the light is off during this gap will vary with the velocity of the segment.
The same will be true of all gaps in the set.
This implies that the signal generated by 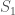 is objectively distinguishable from the signal generated by
is objectively distinguishable from the signal generated by 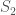 , despite the fact that both will cause the sensor to trigger an infinite number of times.
, despite the fact that both will cause the sensor to trigger an infinite number of times.
This same thought experiment works with any bounded set that has a countable number of “holes” in it.
Note that this (admittedly theoretical) hypothetical suggests that an infinite signal can be conveyed in a finite amount of time.