Computability and Optimization

I’ve developed an optimization algorithm that appears to be universal, in that it can solve superficially totally unrelated problems, e.g., sorting a list, balancing a set of weights, and high-dimensional interpolation. The algorithm itself doesn’t change in any material way, and what changes instead is the statement of what’s being optimized. In the case of a sorted list, I proved that a list is sorted if and only if adjacent terms have minimized distances, which allows sorting to be expressed in terms of optimization (i.e., minimize the distances between adjacent terms). This was not trivial to prove, and I’ve actually never heard of this result before, but more importantly, it suggests the general possibility that all computable problems can be expressed as optimization problems. If this is true, then my optimization algorithm would be able to solve any computable problem, with some non-zero probability. It’s not obvious whether this is true, nor is it obvious that it’s false, so I wouldn’t say it’s a conjecture, it is instead a question. As an example, how would you express Dijkstra’s Algorithm as an optimization problem? I thought about it just a bit, and quickly lost interest because I have too much going on, but the idea is there, and it’s interesting, because if it turns out that all computable problems are equivalent to some optimization problem, then my optimization algorithm has a non-zero probability of solving literally every computable problem. This would make the algorithm a universal problem solving algorithm, which would obviously be useful in A.I., though it already is plainly useful whether or not that’s true, since it can solve a wide class of problems.

Another interesting consequence stems from the observation that this algorithm, and many others, requires a random source (i.e., random number generation). However, a random source is not a feature in a pure UTM, and so it suggests the question of whether a UTM plus a random source is distinct from a UTM alone, and intuition suggests the answer is yes, but this is wrong. Specifically, it seems that a UTM plus a random source can solve problems a UTM alone cannot, which would be theoretically interesting, but is not true. Rather than use a random source, you can instead use a program that exhaustively and iteratively generates all possible values in a problem domain, and use this program to provide the otherwise random inputs to a Monte Carlo type algorithm, which proves equivalence, since every possibility generated by a random source will eventually be generated by the program, that by definition simply generates all possible values in order.

An Apparent Paradox In Probability

I believe it was Gödel who made the statement, “S = S is false”, famous, through his work on the foundations of mathematics, but I’m not completely certain of its history. In any case, it is an interesting statement to consider, because it plainly demonstrates the limitations of logic, which are known elsewhere, e.g., in the case of Turing’s Halting Problem, which similarly demonstrates the limits of computation. You can resolve S by simply barring self-reference, and requiring ultimate reference to some physical system. This would connect logic and reality, and since reality cannot realistically be inconsistent, you shouldn’t have any paradoxical statements in such a system. The Halting Problem however does not have a resolution, it is instead a fundamental limit on computing using UTMs. I discovered something similar that relates to the Uniform Distribution in work my on uncertainty, specifically, this is in Footnote 4 of my paper, Information, Knowledge, and Uncertainty:

“Imagine … you’re told there is no distribution [for some source], in that the distribution is unstable, and changes over time. Even in this case, you have no reason to assume that one [outcome is more] likely than any other. You simply have additional information, that over time, recording the frequency with which each [outcome occurs] will not produce any stable distribution. As a result, ex ante, your expectation is that each [outcome] is equally likely, [since you have no basis to differentiate between outcomes], producing a uniform distribution, despite knowing that the actual observed distribution cannot be a uniform distribution, since you are told beforehand that there is no stable distribution at all.”

From the perspective of pure logic, which is not addressed in the paper, this is an example where the only answer to a problem, is known to be wrong. We can resolve this apparent paradox by saying that there is no answer to the problem, since the only possible answer is also known to be wrong. Nonetheless, it is a bit unnerving, because logic leaves you with exactly one possibility, that is wrong, suggesting the possibility of other problems that have superficially correct answers, that are nonetheless wrong, because of non-obvious, and possibly logically independent considerations. This is not such a problem, because it is actually resolved by simply saying there is no distribution, which is perfectly consistent with the description of the problem, that assumes the distribution is not stable. The point being, that you could have superficially correct answers to some other problem, that are ultimately wrong due to information that you simply don’t have access to.

Probability, Complexity, and Indicia of Sentience

The market tanked about 4.0% this Tuesday, and I naturally searched for causes, like everyone else does, because the event is unlikely, in the sense that most trading days don’t produce such large moves in either direction. But I also acknowledge that it could have been a random outcome, in the most literal sense, that the motion of the S&P 500 was on that day determined by a repeated toll of a random variable, and that’s not something you can simply rule out. Nonetheless, the intuition is there, that low probability events are connected to causation, in the sense that they shouldn’t happen without an intervening cause, simply because they’re so unlikely. This view is however incomplete, and it’s something I’ve commented on in the past, specifically, that what you’re looking to is a property that has a low probability, rather than the event itself. In the case of an asset price, we’d be looking at paths that go basically straight up or straight down, which are few in number, compared to the rest of the paths that generally meander in no particular direction. This can be formalized using one of the first original datasets I put together, that generates random paths that resemble asset prices. In this dataset, there will be exactly two extremal paths that go maximally up and maximally down, and for that reason, those two paths are special, and from a simple counting perspective, there will be exactly two of them out of many.

To continue this intuition with another example, consider sequences generated by repeated coin tosses, e.g., HTH, being the product of flipping heads, then tails, then heads. The probability of any sequence is simply 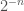, where 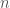is the length of the string, but this fails to capture the surprisal generated by, e.g., producing a sequence that is billions of entries long, and comprised of only heads. If this really happened, you’d be astonished, but it nonetheless is no more or less likely than any other sequence of equal length. As a consequence, measuring surprisal using the Shannon Entropy produces the same result, treating all outcomes equally, because all sequences have equal probabilities. The intuition at work here can instead be formalized using the Kolmogorov Complexity. Specifically, consider all strings of a given length, now calculate the Kolmogorov Complexity of each such string, producing a distribution of complexities. Now your surprisal can be described objectively, since the probability of generating, e.g., an alternating sequence of (HTHTHTH …) of any appreciable length, is also low, just like generating a uniform sequence of (HHHHHHH …) of any appreciable length. The point here, is that what produces surprisal in at least some cases is the Kolmogorov Complexity of an observation, in that large highly structured objects have a low probability over the distribution of complexities, since most strings are Kolmogorov-Random (i.e., have high complexities).

There is moreover, a plain connection between complexity and sentience, because anecdotally, that is generally how large and highly structured objects are produced, i.e., through deliberate action, though this is at times erroneous, since e.g., gravity produces simply gigantic, and highly structured systems, like our Solar System, and gravity is not in any scientific sense, sentient, and instead it has a simple mechanical behavior. However, there is nonetheless a useful, intuitive connection between the Kolmogorov Complexity and sentience, in that as you increase Kolmogorov Complexity from the mundane (e.g., (HHHHH …) or (HTHTHT …)) to the elaborate, but nonetheless patterned, it becomes intuitively more difficult to dismiss the possibility that the sequence was produced by a sentient being, as opposed to being randomly generated. Just imagine e.g., someone telling you that a randomly generated set of pixels produced a Picasso – you would refuse to believe it, justifiably, because highly structured macroscopic objects just don’t get generated that way.

And I’ve said many times, it is simply not credible in this view that life is the product of a random sequence, because that assumption produces probabilities so low, that there’s simply not enough time in the Universe to generate systems as complex as living systems. At the same time, an intervening sentient creator, only produces the same problem, because that sentience would in turn require another sentient creator, and so on. The article I linked to goes through some admittedly imprecise math, that is nonetheless impossible to argue against, but to get the intuition, there are 3 billion base pairs in human DNA. Each base pair is comprised of two selections from four possible bases, adenine (A), cytosine (C), guanine (G) [GWA-NeeN] or thymine (T). Ignoring restrictions, basic combinatorics says there are 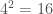possible base pairs. Because there are 3 billion base pairs in human DNA, the total number of possible genetic sequences is , where 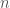is 3 billion. This is a number so large, it cannot be calculated on most machines (e.g., Google cannot calculate it), and for context, the number of seconds since the Big Bang is about (i.e. a number with 18 digits), whereas the number of possible DNA sequences has at least 3 billion digits. Note that while this is plainly rough arithmetic, the number of possible base pairs does not have to be 16 to produce this problem, since if the number of possible base pairs is anything greater than 1 (and it obviously is greater than 1), then you still have a number with roughly billions of digits –

This is a joke of an idea, and instead, I think it is more likely that we just don’t understand physics, and that certain conditions can produce giant molecules like DNA, just like stars produce giant atoms. There is also a branch of mathematics known as Ramsey Theory, that is simply astonishing, and imposes structure on real-world systems, that simply must be there as a function of scale. There could be unknown results of Ramsey Theory, there could be unknown physics, probably both, but I don’t need to know what’s truly at work, since I don’t think it’s credible to say that e.g., DNA is “randomly generated”, as it’s so unlikely as popularly stated, that it’s unscientific.

Finally, in this view, we can make a distinct and additional connection between complexity and sentience, since we all know sentience is real, subjectively, and so it must have an objective cause, which could have something to do with complexity itself, since it seems to exist only in complex systems. Specifically, that once a system achieves a given level of complexity, it gives rise to sentience, as an objective phenomenon distinct from e.g., the body itself. This is not unscientific thinking at all, since it should be measurable, and we already know that certain living systems give rise to poorly understood fields, that are nonetheless measurable. Sentience would in this view be a field generated by a sufficiently complex system, that produces what we all know as a subjective experience of reality itself.