Below I’ll present a vectorized categorization algorithm, and a vectorized prediction algorithm, each of which have a worst-case, low-degree polynomial run time, even in extremely high dimensions. Together, these two algorithms allow for almost instantaneous inferences to be drawn from an enormous number of observations on an ordinary consumer device. As a result, I believe these algorithms will facilitate the commoditization of artificial intelligence, potentially sparking a revolution in the field, and a sea-change in the types of products available to consumers.
Specifically, I’ll show how these algorithms can be used to predict complex random-walks, predict projectile paths in three-dimensions, and classify three-dimensional objects, in each case making use of inferences drawn from millions of underlying data points, all using low-degree polynomial run time algorithms that can be executed on an ordinary consumer device. All of the code necessary to run these algorithms is attached.
Vectorized Categorization and Prediction
In the post below entitled, “Fast N-Dimensional Categorization Algorithm,” I presented a categorization algorithm that can categorize a dataset of N-dimensional vectors with a worst-case run time that is 
, where 
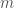is the number of items in the dataset, and 
is the dimension of each vector in the dataset. The categorization algorithm I’ll present in this post is identical to the algorithm I presented below, except this algorithm skips all of the steps that cannot be vectorized. As a result, the vectorized categorization algorithm has a worst-case run time that is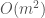 
, where 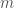is the number of items in the dataset. The corresponding prediction algorithm is basically unchanged, and has a run time that is worst-case 
. This means that even if our underlying dataset contains millions of observations, if it is nonetheless possible to structure these observations as high-dimensional vectors, then we can use these algorithms to produce nearly instantaneous inferences, despite the volume of the underlying data.
As a practical matter, on an ordinary consumer device, the dimension of the dataset will start to impact performance for 
, and as a result, the run time isn’t truly independent of the dimension of the dataset, but will instead depend upon on how the vectorized processes are implemented by the language and machine in question. Nonetheless, the bottom line is that these algorithms allow ordinary, inexpensive consumer devices to almost instantaneously draw complex inferences from millions of observations, giving ordinary consumer devices access to the building blocks of true artificial intelligence.
Predicting Random Paths
Let’s begin by predicting random-walk style data. This type of data can be used to represent the states of a complex system over time, such as an asset price, a weather system, a sports game, the click-path of a consumer, or the state-space of a complex problem generally. As we work through this example, I’ll provide an overview of how the algorithms work, in addition to discussing their performance and accuracy. Note that if you’d like to test any of the data discussed in this article, you can use the scripts I’ve attached, which contain the same code used to generate the training data presented in the examples.
The underlying dataset will in this case consist of two categories of random paths, though the categorization algorithm and prediction algorithm will both be blind to these categories. Specifically, our training data consists of 1,000 paths, each of which contains 10,000 points, for a total of 10,000,000 observations. Of those 1,000 paths, 500 will trend upward, and 500 will trend downward. The index of the vector represents time, and the actual entry in the vector at a given index represents the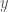 
value of the path at that time. We’ll generate the upward trending paths by making the 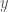value slightly more likely to move up than down as a function of time, and we’ll generate the downward trending paths by making the 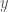value slightly more likely to move down than up as a function of time.
For context, Figure 1 shows both a downward trending path and an upward trending path, each taken from the dataset.
Figure 2 shows the full dataset of 1,000 paths, each of which begins at the origin, and then traverses a random path over 10,000 steps, either moving up or down at each step. The upward trending paths move up with a probability of .52, and the downward trending paths move up with a probability of .48.
After generating the dataset, the next step is to construct two data trees that we’ll use to generate inferences. One data tree is comprised of elements from the original dataset, called the anchor tree, and the other data tree is comprised of threshold values, called the delta tree.
The anchor tree is generated by repeatedly applying the categorization algorithm to the dataset. This will produce a series of subcategories at each depth of application. The top of the anchor tree contains a single nominal vector, and is used by the algorithm for housekeeping. The categories generated by the first application of the categorization algorithm have a depth of 2 in the anchor tree; the subcategories generated by two applications of the categorization algorithm have a depth of 3 in the anchor tree, and so on. The algorithm selects an anchor vector as representative of each subcategory generated by this process. As a result, each anchor vector at a depth of 2 in the anchor tree represents a category generated by a single application of the categorization algorithm, and so on.
As a simple example, assume our dataset consists of the integers {1,2,8,10}. In this case, the first application of the categorization algorithm generates the categories {1,2} {8} {10}, with the anchors being 1, 8, and 10. This is the actual output of the categorization algorithm when given this dataset, and it turns out that, in this case, the algorithm does not think that it’s appropriate to generate any deeper subcategories. For a more detailed explanation of how this whole process works, see the post below entitled, “Predicting and Imitating Complex Data Using Information Theory.”
As a result, in this case, the anchor tree will contain the nominal vector at its top, and then at a depth of 2, the anchors 1,8, and 10 will be positioned in separate entries, indexed by different widths.
Represented visually, the anchor tree is as follows:
(Inf)
(1) (8) (10)
Each application of the categorization algorithm also produces a value called delta, which is the maximum difference tolerated for inclusion in a given category. In the example given above, delta is 1.0538. Specifically, if 
is in a category represented by the anchor vector 
, then it must be the case that 
, where 
is the sufficient difference associated with the category represented by . That is, is the difference between two vectors which, when met or exceeded, we treat as sufficient cause to categorize the vectors separately. The value of delta is determined by making use of processes I’ve developed that are rooted in information theory, but in short, delta is the natural, in-context difference between elements of the category in question. The value has the same depth and width position in the delta tree that the associated anchor vector has in the anchor tree. So in our example above, 1 and 2 are in the same category, since 
, but 8 and 10 are not, since 
.
Since the categorization algorithm is applied exactly once in this case, only one value of delta is generated, resulting in the following delta tree:
(Inf)
(1.0538) (1.0538) (1.0538)
Together, these two trees operate as a compressed representation of the subcategories generated by the repeated application of the categorization algorithm, since we can take a vector from the original dataset, and quickly determine which subcategory it could belong to by calculating the difference between that vector and each anchor, and testing whether it’s less than the applicable delta. This allows us to approximate operations on the entire dataset using only a fraction of the elements from the original dataset. Further, we can, for this same reason, test a new data item that is not part of the original dataset against each anchor to determine to which subcategory the new data item fits best. We can also test whether the new data item belongs in the dataset in the first instance, since if it is not within the applicable delta of any anchor, then the new data item is not a good fit for the dataset, and moreover, could not have been part of the original dataset. Finally, given a vector that contains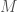 
out of values, we can then predict the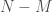 
missing values by substituting those missing values using the corresponding values in the anchors in the anchor tree, and then determining which substitution minimized the difference between the resulting vector and the anchors in the tree.
For example, if 
, and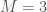 
, then we would substitute the two missing values in the input vector 
, using the last two dimensions of an anchor vector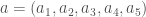 
, producing the prediction vector 
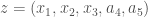. We do this for every anchor in the anchor tree, and test whether 
. If the norm of the difference between the anchor vector and the prediction vector is less than the applicable delta, then the algorithm treats that prediction as a good prediction, since the resulting prediction vector would have qualified for inclusion in the original dataset. As a result, all of the predictions generated by the algorithm will contain all of the information from the input vector, with any missing information that is to be predicted taken from the anchor tree.
This implies that our input vector could be within the applicable delta of multiple anchor vectors, thereby constituting a match for each related subcategory. As a result, the prediction algorithm returns both a single best-fit prediction, and an array of possible-fit predictions. That is, if our input vector produces prediction vectors that are within the applicable delta of multiple anchors, then each such prediction vector is returned in the array of possible fits. There will be, however, one fit for which the difference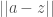 
between the input vector and the applicable prediction vector is minimized, and this is returned by the algorithm as the best-fit prediction vector.
Returning to our example, each path is treated as a 10,000 dimensional vector, with each point in a path represented by a number in the vector. So in this case, the first step of the process will be to generate the data trees populated by repeated application of the categorization algorithm to the dataset of path vectors. Because the categorization algorithm is completely vectorized, this process can be accomplished on an ordinary consumer device, despite the high dimension of the dataset, and the relatively large number of items in the dataset. Once this initial step is completed, we can begin to make predictions using the data trees.
We’ll begin by generating a new, upward trending path, that we’ll use as our input vector, that again consists of 
observations. Then, we’ll incrementally increase 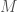, the number of points from that path that are given to the prediction algorithm. This will allow us to measure the difference between the actual path, and the predicted path as a function of 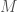, the number of observations given to the prediction algorithm. If 
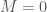, giving the prediction algorithm a completely empty path vector, then the prediction algorithm will have no information from which it can draw inferences. As a result, every path in the anchor tree will be a possible path. That is, with no information at all, all of the paths in the anchor tree are possible.
In this case, the categorization algorithm compressed the 1,000 paths from the dataset into 282 paths that together comprise the anchor tree. The anchor tree has a depth of 2, meaning that the algorithm did not think that subdividing the top layer categories generated by a single application of the categorization algorithm was appropriate in this case. This implies that the algorithm didn’t find any local clustering beneath the macroscopic clustering identified by the first application of the categorization algorithm. This in turn implies that the data is highly randomized, since each top layer category is roughly uniformly diffuse, without any significant in-category clustering.
This example demonstrates the philosophy underlying these algorithms, which is to first compress the underlying dataset using information theory, and then analyze the compressed dataset efficiently using vectorized operations. In this case, since the trees have a depth of 2 and a width of 282, each prediction requires at most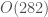 
vectorized operations, despite the fact that the inferences are ultimately derived from the information contained in 
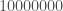observations.
Beginning with 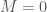observations, each path in the anchor tree constitutes a trivial match, which again can be seen in Figure 2. That is, since the algorithm has no observations with which it can generate an inference, all of the paths in the anchor tree are possible. Expressed in terms of information, when the input information is minimized, the output uncertainty is maximized. As a result, the prediction algorithm is consistent with common sense, since it gradually eliminates possible outcomes as more information becomes available.
Note that we can view the predictions generated in this case as both raw numerical predictions, and more abstract classification predictions, since each path will be either an upward trending path, or a downward trending path. I’ll focus exclusively on classification predictions in another example below, where we’ll use the same categorization and prediction algorithms to predict which class of three-dimensional shapes a given input shape belongs to.
Returning to the example at hand, I’ve set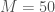 
, and Figure 3 shows the actual path of the new input vector, the average path generated by taking the simple average of all of the predicted paths, and the best-fit path. In this case, the prediction algorithm has only .5% of the path information, and not surprisingly, the average of all predicted paths is flat, since the array of predicted paths contains paths that trend in both directions. In fact, in this case, the array of predicted paths contains the full set of 282 possible paths, implying that the first 50 points in the input path did not provide much information from which inferences can be drawn, though the best-fit path in this case does point in the right direction.
For 
, the actual path, average path, and best-fit path, all clearly trend in the same, correct direction, as you can see in Figure 4. Figure 5 contains the full array of predicted paths for , which consists of 173 possible paths. Though the average path, and best-fit path both point in the correct, upward trending direction, the set of possible paths clearly contains a substantial number of downward trending paths.
Figure 6 shows the average error between the best-fit path and the actual path as a percentage of the 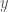value in the actual path, as a function of 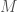. In this case, Figure 6 reflects only the portion of the data actually predicted by the algorithm, and ignores the first 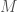points in the predicted path, since the first 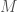points are taken from the input vector itself. That is, Figure 6 reflects only the 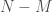values taken from the anchor tree, and not the first 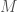values taken from the input vector itself. Also note that the error percentages can and do in this case exceed 100% for low values of .
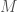As expected, the best-fit path converges to the actual path as 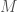increases, implying that the quality of prediction increases as a function of the number of observations. Figure 7 shows the same average error calculation for 25 randomly generated input paths.
Despite the overall convergence of the predictions to the actual path, and the ability of the algorithm to quickly classify an input path as trending upward or downward, this type of data is by its nature incapable of exact prediction. As a result, there is an inherent limit to the precision of any predictions made using this type of data, and the prediction algorithm I’ve presented is no exception, and is, therefore, necessarily going to generate some appreciable amount of error given data that is this randomized. In contrast, in the next section, we’ll predict three-dimensional projectile paths, which allow for tighter predictions.
As noted above, the prediction algorithm is also capable of determining whether a given input vector is a good fit for the underlying data in the first instance. In this case, this means that the algorithm can determine whether the path represented by an input vector belongs to one of the categories in the underlying dataset, or whether the input vector represents some other type of path that doesn’t belong to the original dataset. For example, if we generate a new input vector produced by a formula that has a .55 probability of decreasing at any given moment in time, then for 
, the algorithm returns the nominal vector at the top of the anchor tree as its predicted vector, indicating that the algorithm thinks that the input vector does not belong to any of the underlying categories in the anchor tree.
This ability to not only predict outcomes, but also identify inputs as outside of the scope of the underlying dataset helps prevent bad predictions, since if an input vector is outside of the scope of the underlying dataset, then the algorithm won’t make a prediction at all, but will instead flag the input as a poor fit. This also allows us to expand the underlying dataset by providing random inputs to the prediction function, and then take the inputs that survive this process as additional elements of the underlying dataset. For more on this approach, see the post below entitled, “Predicting and Imitating Complex Data Using Information Theory.”
Categorizations and Predictions in Higher Dimensional Spaces
Predicting Projectile Paths
The same algorithms that we used in the previous section to predict paths in a two-dimensional space can be applied to an N-dimensional space, allowing us to analyze high-dimensional data in high-dimensional spaces. We’ll begin by predicting somewhat randomized, but nonetheless Newtonian projectile paths in three-dimensional space.
In this section, our training data consists of 750 projectile paths, each containing 3000 points in Euclidean three-space, resulting in vectors with a dimension of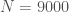 
. The equations that generated the paths in the training data are Newtonian equations of motion, with bounded, but randomly generated x and y velocities, no z velocity other than downward gravitational acceleration, fixed initial x and y positions, and randomly generated, but tightly bounded initial z positions. Figure 8 shows a few of the paths from the dataset.
Note that in this case, we’re predicting a path that has a simple closed form formula without using any interpolation. Instead, the algorithm uses the exact same approach outlined above, which compresses the dataset into a series of anchor vectors, which in this case represent Newtonian paths, and then takes a new curve and attempts to place it in the resulting anchor tree of vectors.
Just as we did above, first we’ll generate a new curve, which will be represented as a 9,000 dimensional vector that consists of 3,000 points in Euclidean three-space. Then, we’ll incrementally provide points from the new curve to the prediction algorithm, and measure the accuracy of the resultant predictions. Figure 9 shows the average path, best-fit path, and actual path for 
.
In this case, the percentage-wise average error between the predicted path and the actual path, shown in Figure 10, is much smaller than it was for the random path data. This is not surprising, given that each curve has a simple shape that is entirely determined by its initial conditions. As a result, so long as there is another curve in the anchor tree that has reasonably similar initial conditions, we’ll be able to accurately approximate, and therefore, predict the shape of the entire input curve.
Shape and Object Classification
We can use the same techniques to categorize three-dimensional objects. We can then take the point data for a new object and determine to which category it best belongs by using the prediction algorithm. This allows us to take what is generally considered to be a hard problem, i.e., three-dimensional object classification, and reduce it to a problem that can be solved in a fraction of a second on an ordinary consumer device.
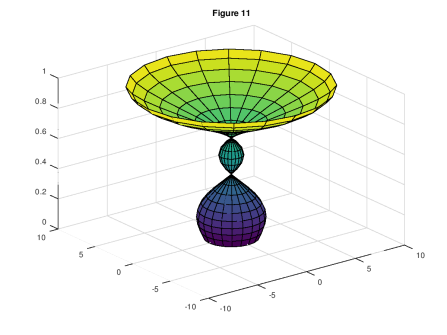
In this case, the training data consists of the point data for 600 objects, each shaped like a vase, with randomly generated widths that come in three classes of sizes: narrow, medium, and wide. That is, each class of objects has a bounded width, within which objects are randomly generated. There are 200 objects in each class, for a total of 600 objects in the dataset. Each object contains 483 points, producing a vector that represents the object with a total dimension of 
. I’ve attached a representative image from each class of object as Figures 11, 12, and 13. Note that the categorization and prediction algorithm are both blind to the classification labels in the data, which are hidden in the 
entry of each shape vector.
As we did above, we’ll generate a new object, provide only part of the point data for that object to the prediction algorithm, and then test whether the prediction algorithm assigns the new object to a category with an anchor from the same class as the input object. That is, if the class of the anchor of the category to which the new input object is assigned matches the class of the input object, then we treat that prediction as a success.
I’ve randomly generated 300 objects from each class as a new input to the prediction algorithm, for a total of 900 input objects. I then provided the first $M = 1200$ values from each input vector to the prediction algorithm, producing 900 predictions. There are three possibilities for each prediction: success (i.e., a correct classification); rejection (i.e., the shape doesn’t fit into the dataset); and failure (i.e., an incorrect classification).
The results for each of the three classes is as follows:
Class One:
Success Percentage: 300 / 300 = 100%.
Rejected Data Percentage: 0 / 300 = 0%.
Fail Percentage: 0 / 300 = 0%.
Class Two:
Success Percentage: 300 / 300 = 100%.
Rejected Data Percentage: 0 / 300 = 0%.
Fail Percentage: 0 / 300 = 0%.
Class Three:
Success Percentage: 300 / 300 = 100%.
Rejected Data Percentage: 0 / 300 = 0%.
Fail Percentage: 0 / 300 = 0%.
These results are of course the product of not only randomly generated training data, but also randomly generated inputs. Different datasets, and different inputs could therefore produce different results. Nonetheless, the obvious takeaway is that the prediction algorithm is extremely accurate.
The Future of Computation
The Church-Turing Thesis is a hypothesis that asserts that all models of computation can be simulated by a Universal Turing Machine. In effect, the hypothesis asserts that any proposed model of computation is either inferior to, or equivalent to, a UTM. The Church-Turing Thesis is a hypothesis, and not a mathematical theorem, but it has turned out to be true for every known model of computation, though recent developments in quantum computing are likely to present a new wave of tests for this celebrated hypothesis.
In a post below entitled, “A Simple Model of Non-Turing Equivalent Computation,” I presented the mathematical outlines of a model of computation that is on its face not equivalent to a UTM. That said, I have not yet built any machines that implement this model of computation, so, not surprisingly, the Church-Turing Thesis still stands.
The simple insight underlying my model is that a UTM cannot generate computational complexity, and this can be proven mathematically (see the link above for a simple proof). This means that the computational complexity (i.e., the Kolmogorov Complexity) of the output of a UTM is always less than or equal to the complexity of the input that generated the output in question. This simple lemma has some alarming consequences, and in particular, it suggests that the behaviors of some human beings might be the product of a non-computable process, perhaps explaining how it is that some people are capable of producing ideas, predictions, and works of art, that appear to come from out of nowhere.
Since we can, as a theoretical matter, map a given input string to an output string 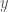that has a higher computational complexity than the input string, any device that actually does this as a physical matter over an infinite set of outputs is by definition not equivalent to a UTM. Expressed symbolically, 
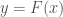, and 
, for some infinite set of outputs 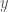, where 
is the Kolmogorov complexity. If the set of possible outputs is infinite, then the device can consistently generate complexity, which is not possible using a UTM. If the device generates only a finite amount of complexity, then the device can of course be implemented by a UTM that has some complexity stored in the memory of the device. In fact, this is exactly the model of computation that I’ve outlined above, where a compressed, specialized tree is stored in the memory of a device, and then called upon to supplement the inputs to the device, generating the outputs of the device.
The model of AI that I’ve presented above suggests that we can create simple, presumably cheap devices, that have specialized memories of the type I described above, that can provide fast, intelligent answers to complex questions, but nonetheless also perform basic computations. This would allow for the true commoditization of artificial intelligence, since these devices would presumably be both small and inexpensive to manufacture. This could lead to a new wave of economic and social changes, where cheap devices, possibly as small as transistors, have the power to analyze a large number of complex observations and make inferences from them in real-time.
In the post below entitled, “Predicting and Imitating Complex Data Using Information Theory,” I showed how these same algorithms can be used to approximate both simple, closed-form functions, and complex, discontinuous functions that have a significant amount of statistical randomness. As a result, we could store trees that implement everyday functions found in calculators, such as trigonometric functions, together with trees that implement complex tasks in AI, such as image analysis, all in a single device that makes use of the algorithms that I outlined above. This would create a single device capable of both general purpose computing, and sophisticated tasks in artificial intelligence. We could even imagine these algorithms being hardwired as “smart transistors” that have a cache of stored trees that are then loaded in real-time to perform the particular task at hand.
All of the algorithms I presented above are obviously capable of being simulated by a UTM, but as a general matter, this type of non-symbolic, stimulus and response computation can in theory produce input-output pairs that always generate complexity, and therefore, cannot be reproduced by a UTM. Specifically, if the device in question maps an infinite number of input strings to an infinite number of output strings that each have a higher complexity than the corresponding input string, then the device is simply not equivalent to a UTM, and its behavior cannot be simulated by a UTM with a finite memory, since a UTM cannot, as a general matter, generate complexity.
This might sound like a purely theoretical model, and it might be, but there are physical systems whose states change in complex ways as a result of simple changes to environmental variables. As a result, if we are able to find a physical system whose states are consistently more complex than some simple environmental variable that we can control, then we can use that environmental variable as an input to the system. This in turn implies that we can consistently map a low-complexity input to a high-complexity output. If the set of possible outputs appears to be infinite, then we would have a system that could be used to calculate functions that cannot be calculated by a UTM. That is, any such system would form the physical basis of a model of computation that cannot be simulated by a UTM, and a device capable of calculating non-computable functions.
Octave Scripts:
optimize_categories_N
generate_data_tree_N
predict_best_fit_tree_N
generate_categories_N
vector_entropy
Data Sets:
Random-Walks
3D Projectile
3D Shape Recognition
generate_random_trials
![W = \sin[\pi (f - f_{min}) / (f_{max}- f_{min})]](https://s0.wp.com/latex.php?latex=W+%3D+%5Csin%5B%5Cpi+%28f+-+f_%7Bmin%7D%29+%2F+%28f_%7Bmax%7D-+f_%7Bmin%7D%29%5D&bg=ffffff&fg=444444&s=0&c=20201002)
![L_P = \log(f) \sin[\pi (f - f_{min}) / (f_{max}- f_{min})]](https://s0.wp.com/latex.php?latex=L_P%C2%A0%3D+%5Clog%28f%29+%5Csin%5B%5Cpi+%28f+-+f_%7Bmin%7D%29+%2F+%28f_%7Bmax%7D-+f_%7Bmin%7D%29%5D&bg=ffffff&fg=444444&s=0&c=20201002)
Information Overload 