I thought I had posted something about the logarithm of  , which is something I think about at times, but I can’t seem to find it, so I’ll begin from scratch:
, which is something I think about at times, but I can’t seem to find it, so I’ll begin from scratch:
Lemma 1. The logarithm of  is not equal to
is not equal to  .
.
Proof. Assume that  . If we assume that
. If we assume that 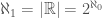 , then it follows that
, then it follows that 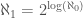 , which leads to a contradiction, since
, which leads to a contradiction, since  .
.
Definitions. As a consequence, I’ve defined a new number,  , that I’ve used in apparently unpublished research to think about the number of bits you’d need to represent a countably infinite system. However, it just dawned on me that you can construct a system that has a number of bits equal to
, that I’ve used in apparently unpublished research to think about the number of bits you’d need to represent a countably infinite system. However, it just dawned on me that you can construct a system that has a number of bits equal to 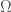 as follows:
as follows:
Assume that a system  is comprised of a countable number of rows, each indexed by the natural numbers, starting with
is comprised of a countable number of rows, each indexed by the natural numbers, starting with 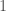 . Now assume that for each row, you have a number of bits equal to the index of the row. So for example, in row
. Now assume that for each row, you have a number of bits equal to the index of the row. So for example, in row 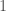 , you have
, you have 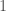 bit, which can be in exactly
bit, which can be in exactly 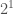 states, and in row
states, and in row 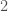 ,
, 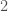 bits, which can be in exactly
bits, which can be in exactly  states, etc. However, assume
states, etc. However, assume  has a tape head, like a UTM, that can move both up and down rows, and left and right, thereby reading or writing to the bits in the row at its current index. So for example, if the head is currently at row
has a tape head, like a UTM, that can move both up and down rows, and left and right, thereby reading or writing to the bits in the row at its current index. So for example, if the head is currently at row 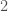 , it can move left or right, to access the
, it can move left or right, to access the 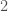 bits that are in that row. Further, assume that if the head moves either up or down, then all of the bits in every row reset to zero. So this means that once the tape head changes rows, all of the information in the entire system is effectively deleted.
bits that are in that row. Further, assume that if the head moves either up or down, then all of the bits in every row reset to zero. So this means that once the tape head changes rows, all of the information in the entire system is effectively deleted.
The number of states that  can occupy is at least
can occupy is at least  , since it can represent every natural number. However,
, since it can represent every natural number. However,  is distinct from a countably infinite binary string, since changing the row of the tape head causes the entire system to reset, which implies that only a finite number of bits, all within a single row, can ever be used in combination with one another. The number of bits in
is distinct from a countably infinite binary string, since changing the row of the tape head causes the entire system to reset, which implies that only a finite number of bits, all within a single row, can ever be used in combination with one another. The number of bits in  is therefore unbounded, but not equal to
is therefore unbounded, but not equal to  , because they cannot be used in combination with one another, outside of a single row.
, because they cannot be used in combination with one another, outside of a single row.
Lemma 2. The number of states of  cannot be greater than
cannot be greater than  .
.
Proof. We can assign finite, mutually exclusive subsets of 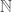 to each row
to each row  of
of  with a cardinality of at least
with a cardinality of at least 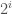 (e.g., use mutually exclusive subsets of powers of primes). Therefore, the number of states of
(e.g., use mutually exclusive subsets of powers of primes). Therefore, the number of states of  cannot be greater than the number of elements in
cannot be greater than the number of elements in 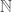 , which is equal to
, which is equal to  .
.
Corollary 3. The number of states of  is equal to
is equal to  .
.
Proof. Every natural number corresponds to at least one state of  , which implies that the number of states of
, which implies that the number of states of  is at least
is at least  . However, Lemma 2 implies that the number of states of
. However, Lemma 2 implies that the number of states of  cannot be greater than
cannot be greater than  , which implies that they are equal.
, which implies that they are equal.
Assumption. The number of bits in a system is equal to the logarithm of the number of states of the system.
This is a standard assumption for finite systems, since it implies that a system with  states is equivalent to
states is equivalent to  bits. In this case, it implies that
bits. In this case, it implies that  is equivalent to
is equivalent to  bits, since
bits, since  has exactly
has exactly  states, just like the set of natural numbers itself.
states, just like the set of natural numbers itself.
Lemma 4. 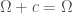 , for all
, for all  .
.
Proof. Assume 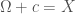 . It follows that
. It follows that  , which implies
, which implies 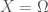 .
.
Corollary 5.  .
.
Proof. This follows immediately from Lemma 4, since there is no such natural number.
Note that 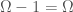 , which in turn implies that we can remove any single row from
, which in turn implies that we can remove any single row from  , without reducing the number of bits in
, without reducing the number of bits in  , which is clearly the case.
, which is clearly the case.
Corollary 6.  .
.
Proof. We can assign finite, mutually exclusive subsets of 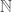 to each row
to each row  of
of  with a cardinality of at least
with a cardinality of at least  (e.g., use mutually exclusive subsets of powers of primes). Therefore, the number of bits in
(e.g., use mutually exclusive subsets of powers of primes). Therefore, the number of bits in  cannot be greater than the number of elements in
cannot be greater than the number of elements in 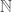 , which is equal to
, which is equal to  . However, Lemma 1 implies that
. However, Lemma 1 implies that 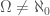 , and therefore,
, and therefore,  .
.
Corollary 7.  , for all
, for all 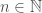 .
.
Proof. For any given 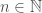 , we can always find a row
, we can always find a row  of
of  such that
such that  . Therefore, the number of bits in
. Therefore, the number of bits in  is greater than
is greater than 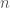 , for all
, for all 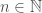 .
.
Corollary 8. There is no set  with a cardinality of
with a cardinality of 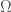 .
.
Proof. Assume such a set 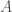 exists. Because
exists. Because  , for all
, for all 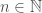 ,
,  cannot be finite. Because
cannot be finite. Because  ,
, 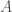 cannot be countable. All subsets of
cannot be countable. All subsets of 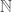 are comprised of either a finite, or countable number of elements, which completes the proof.
are comprised of either a finite, or countable number of elements, which completes the proof.
So to summarize, the number of bits in  is sufficient to represent all natural numbers, and the number of states of
is sufficient to represent all natural numbers, and the number of states of  is equal to the cardinality of the natural numbers. If we assume as a general matter, that the number of bits in a system is equal to the logarithm of the number of states of the system, then the number of bits in
is equal to the cardinality of the natural numbers. If we assume as a general matter, that the number of bits in a system is equal to the logarithm of the number of states of the system, then the number of bits in  is
is  .
.
Corollary 9. There is no number of bits  , such that
, such that  , for all
, for all 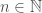 .
.
Proof. Assume that such a number exists, and that for some system  , the number of states of
, the number of states of  is
is  . If
. If  , then
, then 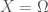 , which leads to a contradiction, so it must be the case that
, which leads to a contradiction, so it must be the case that  . Because
. Because  , the number of states of
, the number of states of  must be less than the number of states of
must be less than the number of states of  , and so
, and so 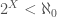 . This implies that we can assign each state of
. This implies that we can assign each state of  a unique natural number, which in turn implies the existence of a set of natural numbers
a unique natural number, which in turn implies the existence of a set of natural numbers 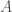 , such that
, such that  , for all
, for all 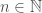 , and
, and 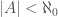 . Since the existence of
. Since the existence of  implies the existence of
implies the existence of 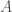 , which leads to a contradiction,
, which leads to a contradiction,  does not exist.
does not exist.
Corollary 10. There is no set 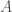 such that
such that  .
.
Proof. Assume such a set 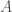 exists. Since
exists. Since  , we can assign each element of
, we can assign each element of 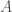 a unique natural number, which will in the aggregate generate a set
a unique natural number, which will in the aggregate generate a set 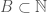 . The existence of
. The existence of 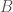 contradicts Corollary 8, which completes the proof.
contradicts Corollary 8, which completes the proof.
This work implies that 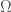 is the smallest non-finite number, and that it does not correspond to the cardinality of any set.
is the smallest non-finite number, and that it does not correspond to the cardinality of any set.
This in turn implies an elegant theory of number itself:
Begin with a system 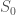 , that is always in the same state
, that is always in the same state 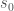 , and assume that the number of states of
, and assume that the number of states of 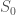 is
is 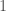 , and that the number of bits in
, and that the number of bits in 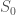 is
is 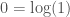 . Now assume the existence of
. Now assume the existence of 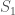 , that is always in the same state
, that is always in the same state 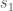 , and that this state is distinct from
, and that this state is distinct from 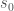 . Further, assume the existence of some system
. Further, assume the existence of some system  that can be in either
that can be in either 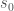 or
or 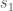 , and assume that the number of states of
, and assume that the number of states of  is
is 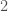 , and that the number of bits in
, and that the number of bits in  is
is  . If we allow for unbounded instances of
. If we allow for unbounded instances of  to exist in conjunction with one another, then basic counting principles imply the existence of all natural numbers, since a collection of systems, each equivalent to
to exist in conjunction with one another, then basic counting principles imply the existence of all natural numbers, since a collection of systems, each equivalent to  , is in turn equivalent to some binary string.
, is in turn equivalent to some binary string.
Note that in this view, the number 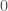 always has units of bits, and is never some number of states, just like
always has units of bits, and is never some number of states, just like 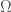 must always have units of bits, since it does not correspond to the cardinality of any set, or number of states. It suggests the notion that some numbers must necessarily cary particular units, because they can only be derived from one class of mathematical object, that necessarily implies those units. For example, in this view,
must always have units of bits, since it does not correspond to the cardinality of any set, or number of states. It suggests the notion that some numbers must necessarily cary particular units, because they can only be derived from one class of mathematical object, that necessarily implies those units. For example, in this view, 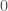 must always carry units of bits, and can never cary units of states. In contrast,
must always carry units of bits, and can never cary units of states. In contrast, 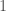 can be either a number of bits, or a number of states.
can be either a number of bits, or a number of states.
Interestingly, Shannon’s equation implies that the logarithm of the reciprocal of a probability,  has units of bits. The work above implies that the logarithm of some number of states,
has units of bits. The work above implies that the logarithm of some number of states,  also has units of bits. Together, this implies that a probability has units of the reciprocal of some number of states,
also has units of bits. Together, this implies that a probability has units of the reciprocal of some number of states, 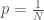 . This is perfectly consistent with a frequentist view of a probability, which would be expressed as some portion of some number of states. Again, all of this work suggests the possibility that numbers have intrinsic units, apart from any physical measurement.
. This is perfectly consistent with a frequentist view of a probability, which would be expressed as some portion of some number of states. Again, all of this work suggests the possibility that numbers have intrinsic units, apart from any physical measurement.















